Zbiór Cantora – podzbiór prostej rzeczywistej opisany w 1883[1] przez niemieckiego matematyka Georga Cantora. Zbiór ten odkrył w 1875 Henry John Stephen Smith[2]. Zbiór Cantora jest najprostszym przykładem fraktala. Topologicznym zbiorem Cantora nazywa się każdą przestrzeń topologiczną homeomorficzną z trójkowym zbiorem Cantora
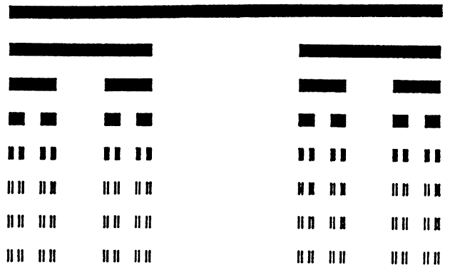
Zbiór Cantora jest tworzony przez iteracyjne usuwanie otwartej środkowej tercji z zestawu segmentów linii. Jeden zaczyna się od usunięcia otwartej środkowej trzeciej ( 1 / 3 , 2 / 3 ) z przedziału [0, 1], pozostawiając dwa odcinki linii: [0, 1 / 3 ] ∪ [ 2 / 3 , 1]. Następnie otwarta środkowa trzecia część każdego z pozostałych segmentów jest usuwana, pozostawiając cztery segmenty linii: [0, 1 / 9 ] ∪ [ 2 / 9 , 1 / 3 ] ∪ [ 2 / 3 , 7 / 9 ] ∪ [ 8 / 9 , 1]. Ten proces jest kontynuowany w nieskończoność , gdzie znajduje się n- ty zbiór Zbiór trójskładnikowy Cantora zawiera wszystkie punkty w przedziale [0, 1], które nie są usuwane na żadnym etapie tego nieskończonego procesu